Applicazioni di Intelligenza Artificiale - CLP

Prof. Marco Gavanelli

17 luglio 2013

Esercizio (8 punti)

Una rete logica è costituita da porte AND e OR, collegate come in un albero binario. La rete è descritta nel file rete1.pl .

Il file contiene dei fatti

dove

• NodoPadre è un numero intero che rappresenta il nodo
• TipoPorta è il tipo di porta e può essere and oppure or
• Figlio1 e Figlio2 sono gli identificatori dei nodi figli.

Ad esempio, il fatto

vuol dire che il nodo 1 è l'AND dei valori sui nodi 2 e 3.

Il file rete1.pl contiene anche dei fatti

che rappresentano le foglie dell'albero.

• Nodo è l'identificatore del nodo
• Valore può essere 0 o 1, dove 0 sta per FALSO e 1 per VERO (logica positiva).

Ad esempio, i fatti:

tree(1,and,2,3).
tree(2,or,4,5).
tree(3,or,6,7).
tree(4,or,8,9).
leaf(5,1).
leaf(6,0).
leaf(7,1).
leaf(8,0).
leaf(9,1).

rappresentano la rete riportata in figura:

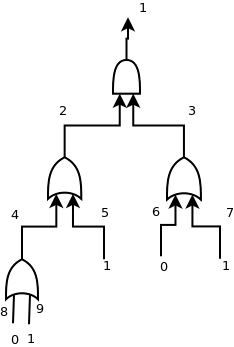
Il nodo 1 è sempre la radice dell'albero (il valore di output della rete combinatoria). Dati i valori di ingresso delle foglie, è possibile calcolare il valore di uscita sul nodo 1; nell'esempio in figura l'output è 1.

Il valore in output, però, non è quello che voleva ottenere il progettista; il valore che voleva ottenere è riportato nel file rete1.pl nel fatto

Si scriva un programma CLP(FD) che calcola qual è il numero minimo di porte che bisogna cambiare (da AND a OR o viceversa) perché il nodo 1 fornisca il risultato nel fatto result.

Nell'esempio in figura, se si ha il fatto result(0), si dovrà calcolare qual è il numero minimo di porte da sostituire per ottenere il valore 0 sul nodo 1 (in questo esempio viene 1, perché basta sostituire la porta che ha come output il nodo 3).

Soluzione

:- lib(fd).
:- lib(fd_global).
:- lib(propia).
:- [rete1].

change(Changes,LNodi):-
	result(V),
	vincoli(1,Bools,V,Changes,LNodi),
	sumlist(Changes,Nchange),
	append(Bools,Changes,Vars),
	minimize(labeling(Vars),Nchange).

vincoli(Nodo,[V],V,[],[]):-
	leaf(Nodo,V),!.
vincoli(Nodo,[V|Bools],V,[Change|Changes],[Nodo|LNodi]):-
	tree(Nodo,OP,A,B),!,
	vincoli(A,BoolsA,VA,ChangesA,LNodiA),
	vincoli(B,BoolsB,VB,ChangesB,LNodiB),
	and_or(OP,VA,VB,V,Change) infers most,
	append(BoolsA,BoolsB,Bools),
	append(ChangesA,ChangesB,Changes),
	append(LNodiA,LNodiB,LNodi).
% La lista LNodi serve solo per interpretare il risultato:
% Serve per capire dall'output quali sono le porte che sono state cambiate

% and_or(TipoPorta,A,B,V,Cambiato)
% se Cambiato = 0, V e` il risultato della porta TipoPorta
% se Cambiato = 1, V e` il risultato della porta opposta
and_or(and,A,B,V,0):- minlist([A,B],V). % Oppure: #/\(A,B,V)
and_or(and,A,B,V,1):- maxlist([A,B],V).
and_or(or,A,B,V,0):- maxlist([A,B],V).
and_or(or,A,B,V,1):- minlist([A,B],V).