Programma a.a. 2008-09
(prof. P. Codecà, a.a. 2008/09)
Clicca qui per scaricare il programma in formato .pdf
- Rappresentazione dei numeri in base b
(è richiesta la dimostrazione nel caso dei numeri naturali, mentre è sufficiente l’enunciato dei teoremi per i numeri reali)
- Insiemi finiti, infiniti, numerabili e non numerabili
Definizioni.
Numerabilità di 
N x N.
Numerabilità delle unioni numerabili di insiemi numerabili.
Numerabilità di Q e non numerabilità di R (sono richieste le dimostrazioni)
- Curve in Rn
Definizioni.
Rettificabilità e lunghezza.
Curve equivalenti.
Curve in funzione dell’arco.
Integrali curvilinei.
(Sono sufficienti le definizioni)
- Campi vettoriali
Campi n-dimensionali.
Definizioni di potenziale e lavoro.
Campi conservativi e loro proprietà.
Definizione di rotore.
(Sono richieste due dimostrazioni: precisamente:
i) indipendenza del lavoro dal cammino che congiunge due punti (per i campi conservativi),
ii) irrotazionabilità dei campi conservativi).
Un esempio importante: il campo gravitazionale.
- Formule di Green
Le formule di Green ed il teorema della divergenza (caso bidimensionale).
(Sono richieste le dimostrazioni)
- Serie trigonometriche
Il sistema trigonometrico.
Definizioni di sistema ortogonale e ortonormale.
I coefficienti di Fourier.
Proprietà di minimo dei coefficienti di Fourier (con dimostrazione).
Disuguaglianza di Bessel (con dimostrazione).
L'identità di Parseval (solo enunciato).
Sviluppi in serie di Fourier (solo l’enunciato del teorema).
- La ricorsività lineare omogenea di grado due
Il concetto di funzione generatrice.
Il teorema che fornisce la “forma chiusa” della sequenza ricorsiva definita da u0=u0,
u1=u1, un= aun-1 + bun-2 ∀ n
2.
(E’ richiesta la dimostrazione solo nel caso delle radici distinte).
Un esempio importante (anche storicamente): i numeri di Fibonacci.
- La ricorsività non lineare
Il problema delle parentesi di Catalàn e la sua soluzione. (Dimostrazione facoltativa)
- Ricorsività e sequenze pseudo-casuali di tipo aritmetico
i) Prerequisiti aritmetici
Definizione di divisore e di numero primo.
Il teorema fondamentale dell’Aritmetica (solo enunciato).
Definizione e proprietà elementari delle congruenze.
Sistemi completi e sistemi ridotti di resti. Loro proprietà.
La legge di cancellazione.
Il teorema di Eulero-Fermat (con dimostrazione).
Soluzione delle congruenze di primo grado (con dimostrazione)
Il concetto di ordine.
Proprietà dell’ordine.
Definizione di radice primitiva mod m
Definizione di gruppo.
Gruppi ciclici.
Esempi aritmetici.
ii) Sequenze (pseudo) casuali generate con il metodo delle congruenze lineari
La sequenza ricorsiva x0=x0, xn+1≡axn+c (mod m).
La forma equivalente xn≡anx0+c (1+a+a2+……+an-1) (mod m) (con dimostrazione).
Il caso x0=0, c=1.
Studio delle sequenze rappresentative da detta formula (è richiesta la dimostrazione solo nel caso m=p, modulo primo)
- Misure di Peano-Jordan
Definizione di intervallo in Rp e di insieme elementare: loro misura.
Definizione di misura interna e misura esterna per sottoinsiemi limitati di Rp.
Definizione di misura per un sottoinsieme A 
incluso in Rp.
Legami tra misura esterna, misura interna e misura della frontiera (δA) di un sottoinsieme
A incluso in Rp , cioè miseA= misiA + mise δA (senza dim).
Misurabilità dei trapezoidi relativi a funzioni monotone. (con dimostrazione)
Non misurabilità (secondo Peano-Jordan) dell’insieme:
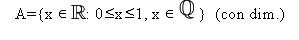
- Misura di Lebesgue (tutto senza dim.)
Definizione di anello e di σ-anello.
La famiglia Σ degli insiemi elementari.
Definizione di misura regolare.
Definizione di misura esterna per sottoinsiemi A incluso in Rp.
La misura esterna prolunga la misura su Σ ed è sub additiva (senza dim)
Definizione di misura di Lebesgue. (solo l’enunciato del teorema 3)
12. Confronto tra le misure di Peano-Jordan e di Lebesgue
Ogni sottoinsieme A incluso in Rp misurabile secondo Peano-Jordan lo è anche secondo Lebesgue e la misura è la stessa (senza dim.).
Misurabilità (con misura nulla secondo Lebesgue) degli insiemi misurabili (con dimostrazione).
13 . Integrale di Lebesgue (tutto senza dim)
Definizione di spazio misurabile e di funzione misurabile.
Esempi di funzioni misurabili (funzioni continue, funzione di Dirichlet….).
Misurabilità di |f| se f è misurabile e misurabilità di massimi e minimi limiti di successioni di funzioni misurabili.
Definizioni di funzione caratteristica e di funzione semplice.
14. Integrazione secondo Lebesgue
Definizione di integrale per le funzioni semplici.
Definizione di integrale per le funzioni misurabili.
Proprietà dell’integrale.
Teorema della convergenza monotona o di Beppo Levi (solo enunciato).
Teorema della convergenza dominata (solo enunciato).
Confronto tra l’integrale di Riemann e di Lebesgue (solo enunciato).
